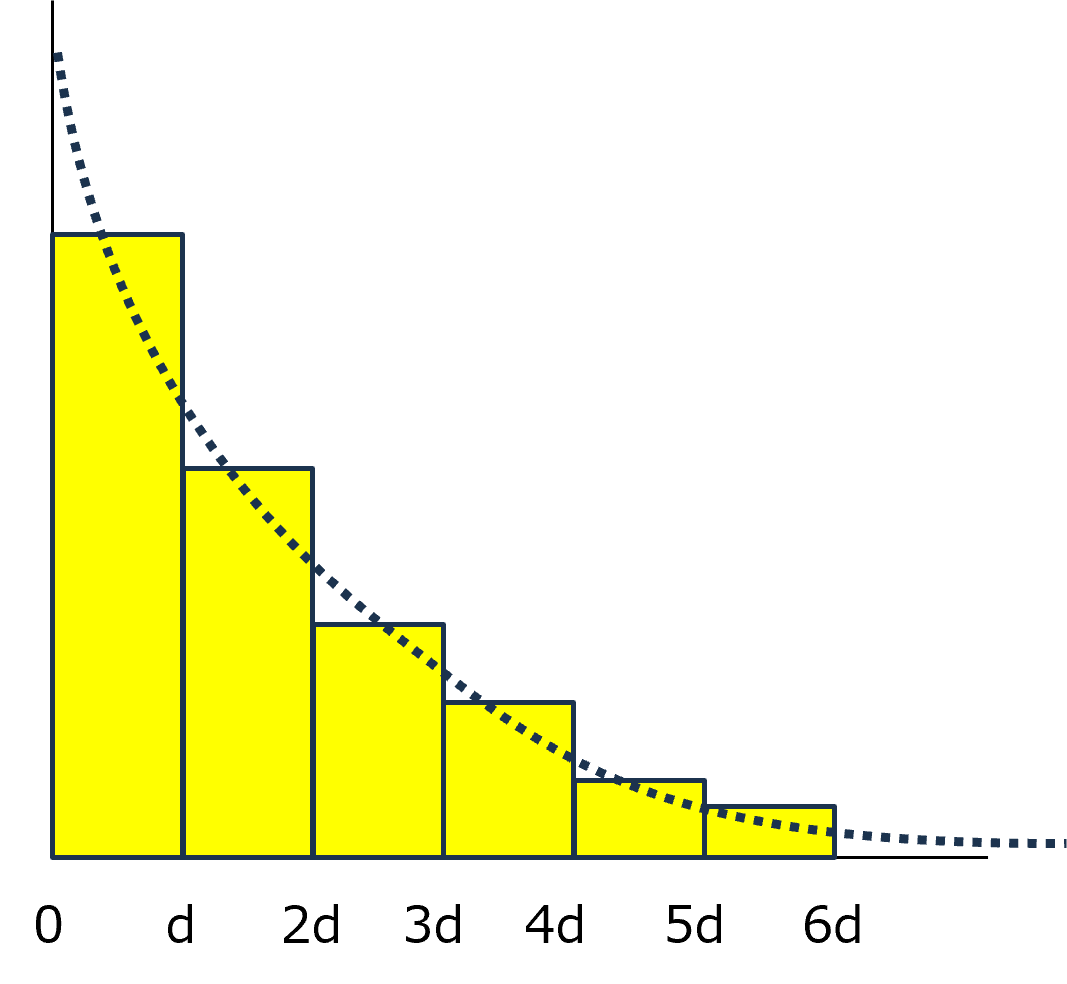
・単一指数関数
単一指数関数の確率密度は,
\(\Large \displaystyle P(x) = k \ exp (-k \ x) \)
です.この場合の累積密度関数は,
\(\Large \displaystyle \int_0^x k \ exp (-k \ x') dx' = -\frac{k}{k} \left[ exp (-k \ x') \right]_0^x = 1 - exp (-k \ x) \)
となります.
解法1:
累積密度関数で推定したパラメータを基に,ヒストグラムを作成した場合,

この図のように,bin(d)ごとに集計します.
その総和は推定したデータ数,N,となりますので,
\(\Large \displaystyle N = C \cdot \sum_{i=0}^\infty \left[ exp (-k \ d \ i) \right] \)
となります,このCを求めたいわけです.
\(\Large \displaystyle y = \sum_{i=0}^\infty \left[ exp (-k \ d \ i) \right] = 1 + exp (-k \ d) + exp (-2 k \ d) + exp (-3 k \ d)...... \)
\(\Large \displaystyle y \cdot exp (-k \ d) = \hspace{74 pt} exp (-k \ d) + exp (-2 k \ d) + exp (-3 k \ d)...... \)
となるので,二つの式の引き算をとると,
\(\Large \displaystyle y - y \cdot exp (-k \ d) =1 \)
\(\Large \displaystyle y =\frac{1}{1- exp (-k \ d)} \)
となるので,
\(\Large \displaystyle N = C \cdot \frac{1}{1- exp (-k \ d)} \)
となり,結局Cは,
\(\Large \displaystyle C = N \cdot [ 1- exp (-k \ d) ] \)
となるので,ヒストグラムは,Cの高さを基準にした指数関数となります.
解法2:
指数関数で表した場合,0~dの割合は,
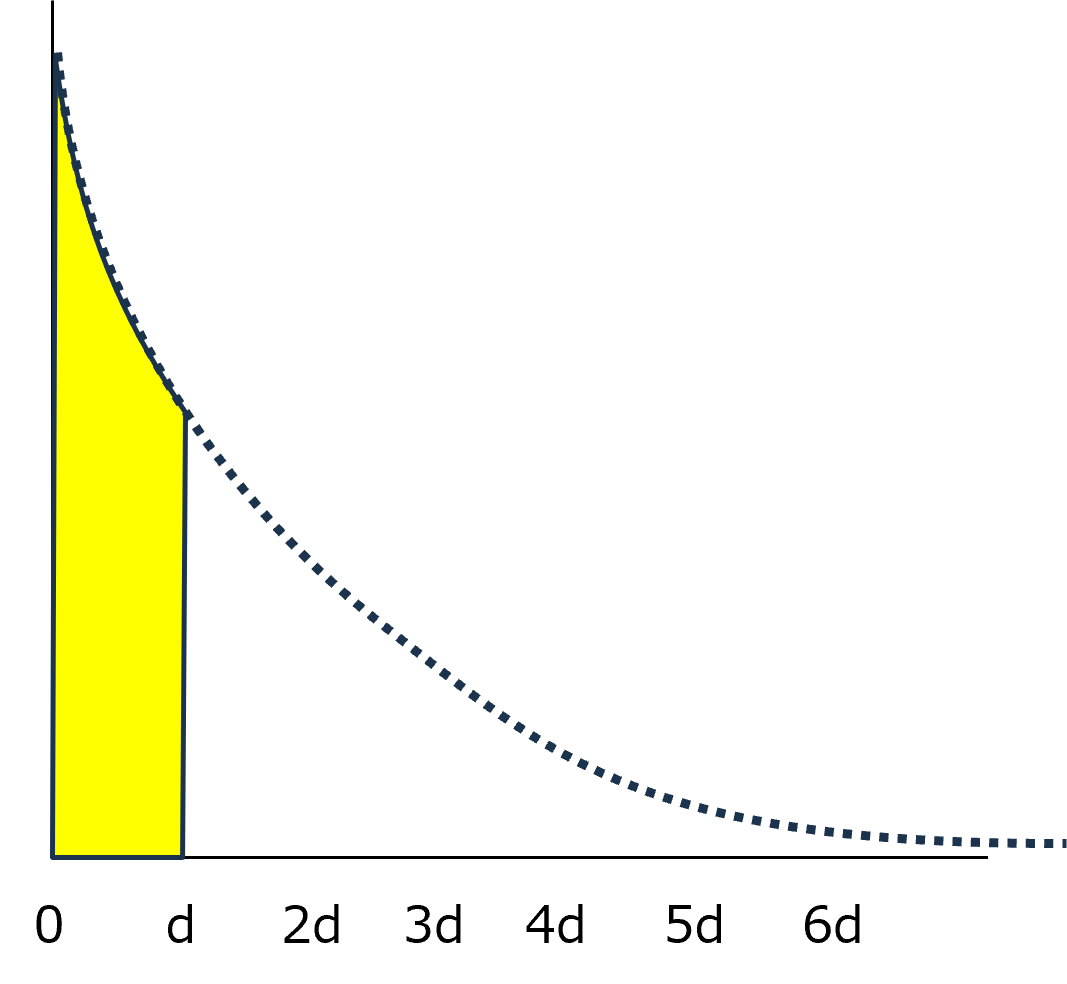
\(\Large \displaystyle \int_0^d exp (-k \ x) \ dx = -\frac{k}{k} \left[ exp (-k \ x) \right]_0^d = 1- exp (-k \ d)\)
となるので,全体の数,N,のうち
\(\Large \displaystyle N \cdot [1- exp (-k \ d) ] \)
が基準となります.
・実際の計算
実際に,ランダム関数から指数分布を作成して(詳細はここ),k,dを色々変えて計算させると,
k=0.1, d=1, N=1000, -> 95.16
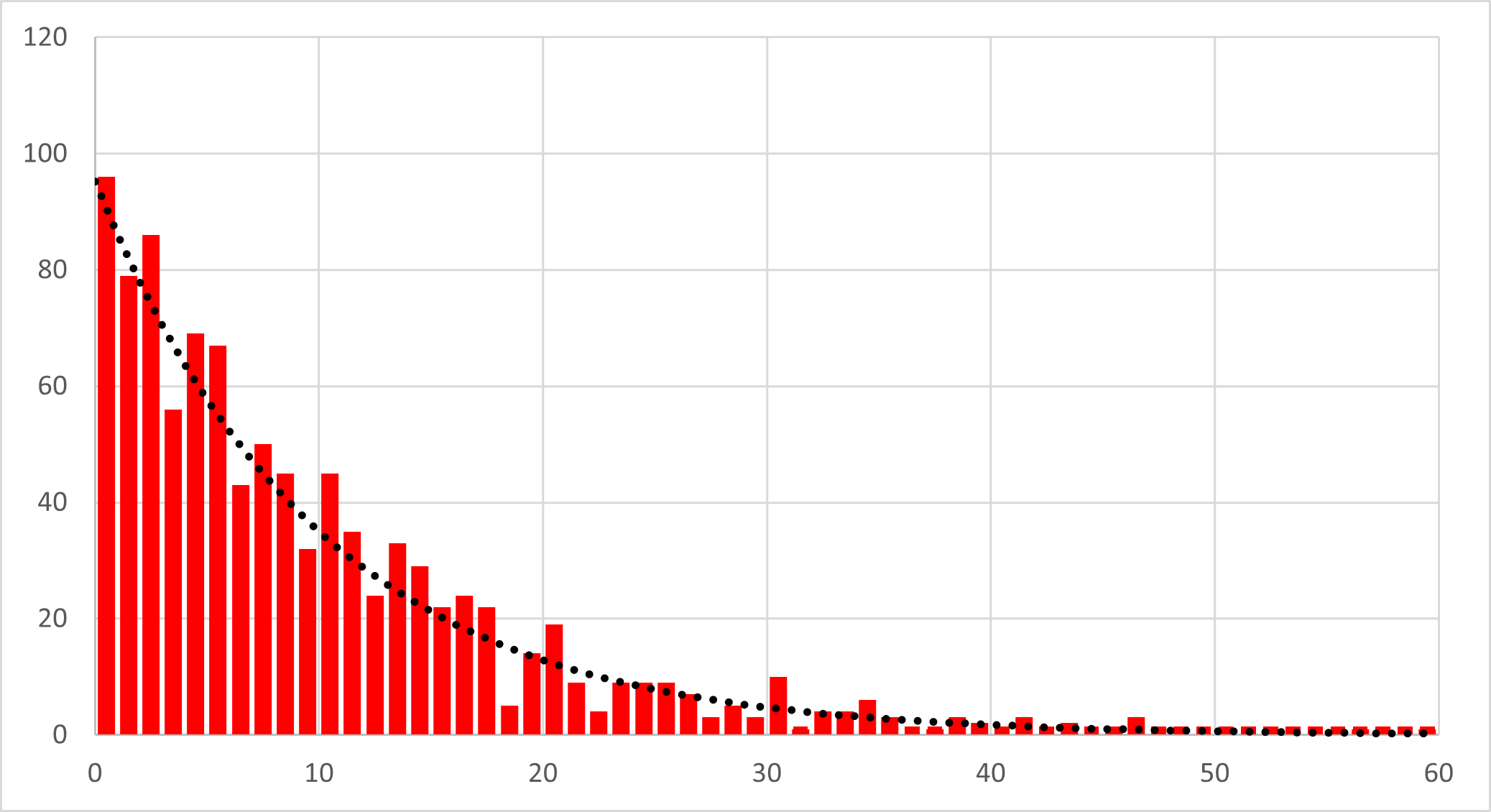
k=0.1, d=0.5, N=1000, -> 48.77
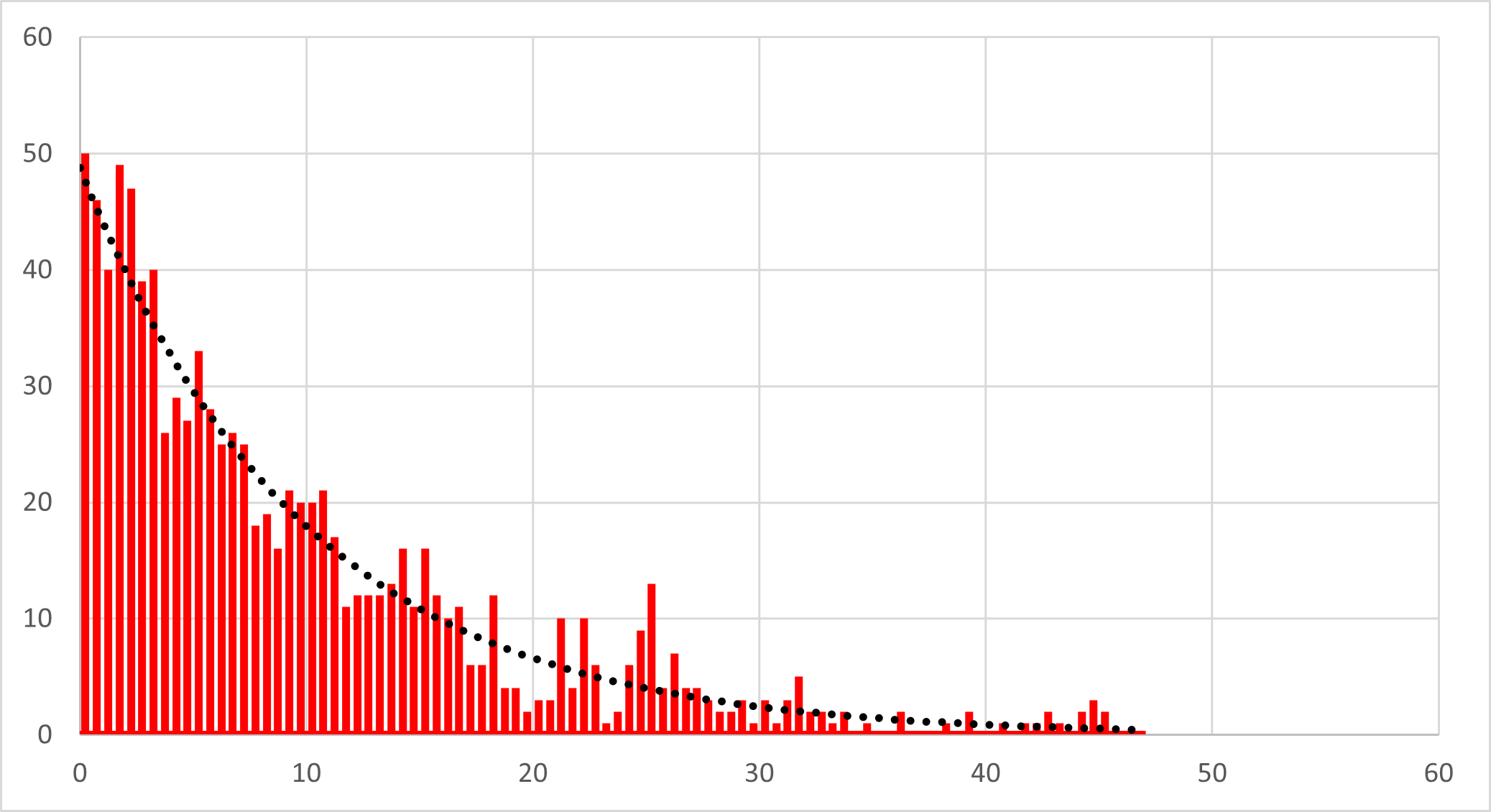
k=0.2, d=0.5, N=1000, -> 95.16
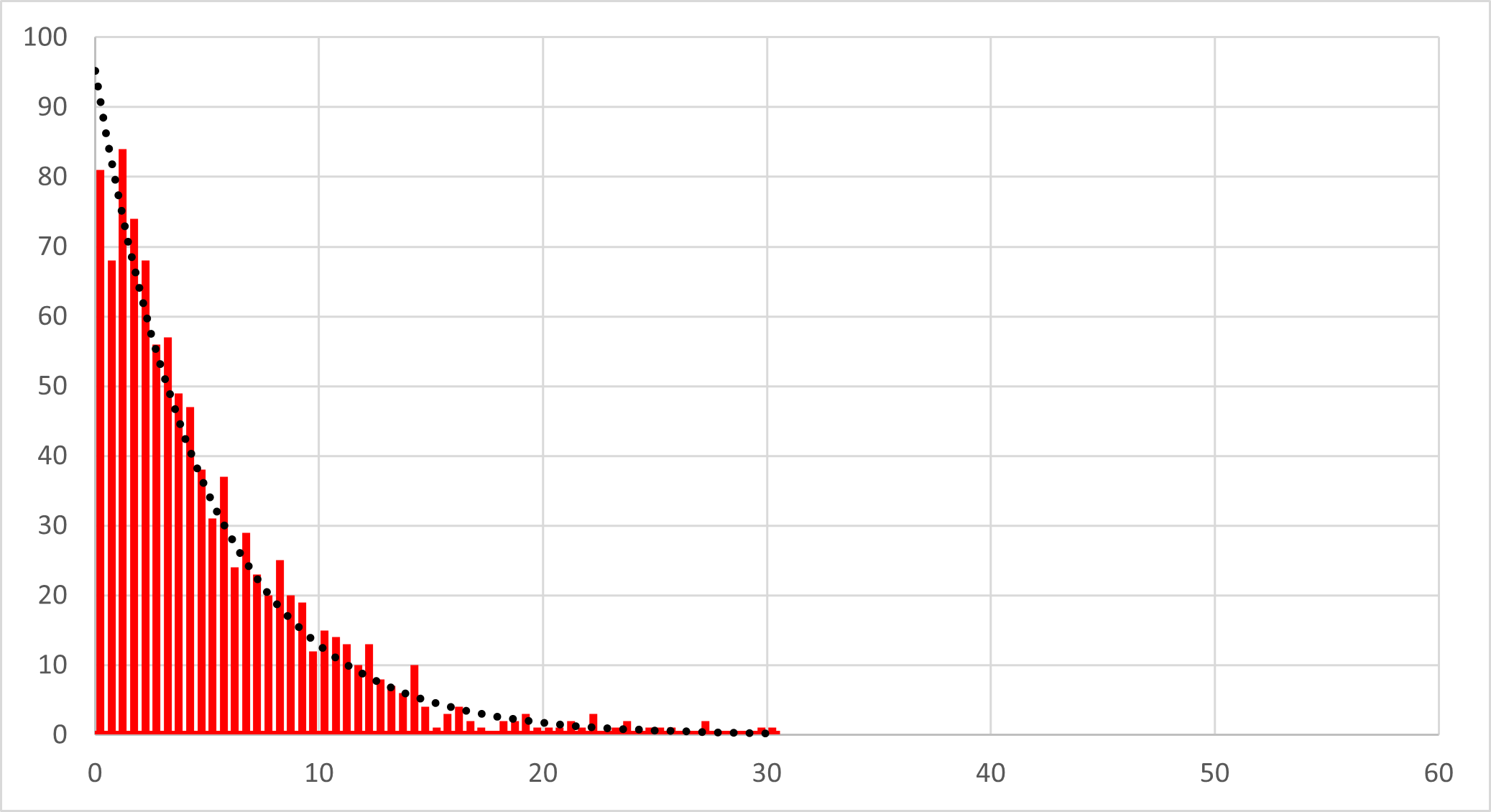
ときれいにフィットできました.
ちなみに,エクセルで散布図で棒グラフを作る方法は,ここ,を参考にしました.
短いデータが欠損している場合
ここ,で説明しているように,累積関数でのフィットは短いデータが欠損している場合に有効です.
その際には,
\(\Large \displaystyle \frac{ [A_0]}{k} \cdot \left( 1 - e^{-kt} \right) + D \)
でフィットできることを示しました.書き換えると,
\(\Large \displaystyle N_1 \cdot \left( 1 - e^{-kt} \right) + N_2 \)
という関数で表すことができます.ここで,ヒストグラムにフィットさせる場合には,欠損しているデータ数も加えなくてはならないので,
\(\Large \displaystyle N = N_1 + N_2 \)
として計算することになります.
次は,二つの指数関数の和,の場合です.